PROCJAM 2024

PROCJAM—the procedural generation (Procgen) jam where people make things that make things—is back for its 2024 edition. I set some time aside this week to figure out whether there is any Procgen potential in Tangram—a puzzle game from 18th-century China.

I rediscovered a wooden Tangram set last year, when I helped my parents declutter and move, and instantly remembered how this unimposing toy fascinated me as a kid. Today I understand that this is the same kind of fascination that brought me to Procgen: Systems with small rule sets that can produce very complex outputs spark joy and my urge to explore. (Which, coincidentally, is also the reason why current “AI” and large language models do not impress me at all: complex things done by complex systems is just not that jaw-dropping.)

A wooden Tangram set with seven pieces, box, and instruction booklet laid out on my desk.

The goal of the puzzle is to replicate an outlined shape using all seven pieces, also called tans, without overlap.

A typical Tangram puzzle: An outline of a key on the right, the solution how to combine the seven tans to form the key on the right.

A couple of questions that popped into my head when I started thinking about Tangram’s potential for this game jam:

I am convinced: There is something to gain from modeling this puzzle game and casting it in code.

2024-10-26: Doodling and Hard-Coded Configurations

My first task is to model tans, be able to draw tans to the screen, and create hard-coded (as in: place tans with set coordinates on the screen) configurations. In this explorative phase, I am using the p5.js web editor and you can tinker with my code.

I think we need the following information to properly describe a tan:

That way we can translate, rotate, and reflect. The latter is only needed for the parallelogram, as this is the only piece without reflection symmetry. We are able to flip the wooden piece around in real life, so we need to be able to model that in code as well. All the other tans are axisymmetric, i.e. reflection or “flipping around” can be modeled by rotation. The set of vertices allows me to draw the tan onto the screen.

Side note: My Remarkable 2 has proven to be an indispensable tool in this early stage of the project; allowing me to scribble, turn handwritten into typed text, and move and rotate selected areas of the page massively helped me grokking the linear algebra behind all this.

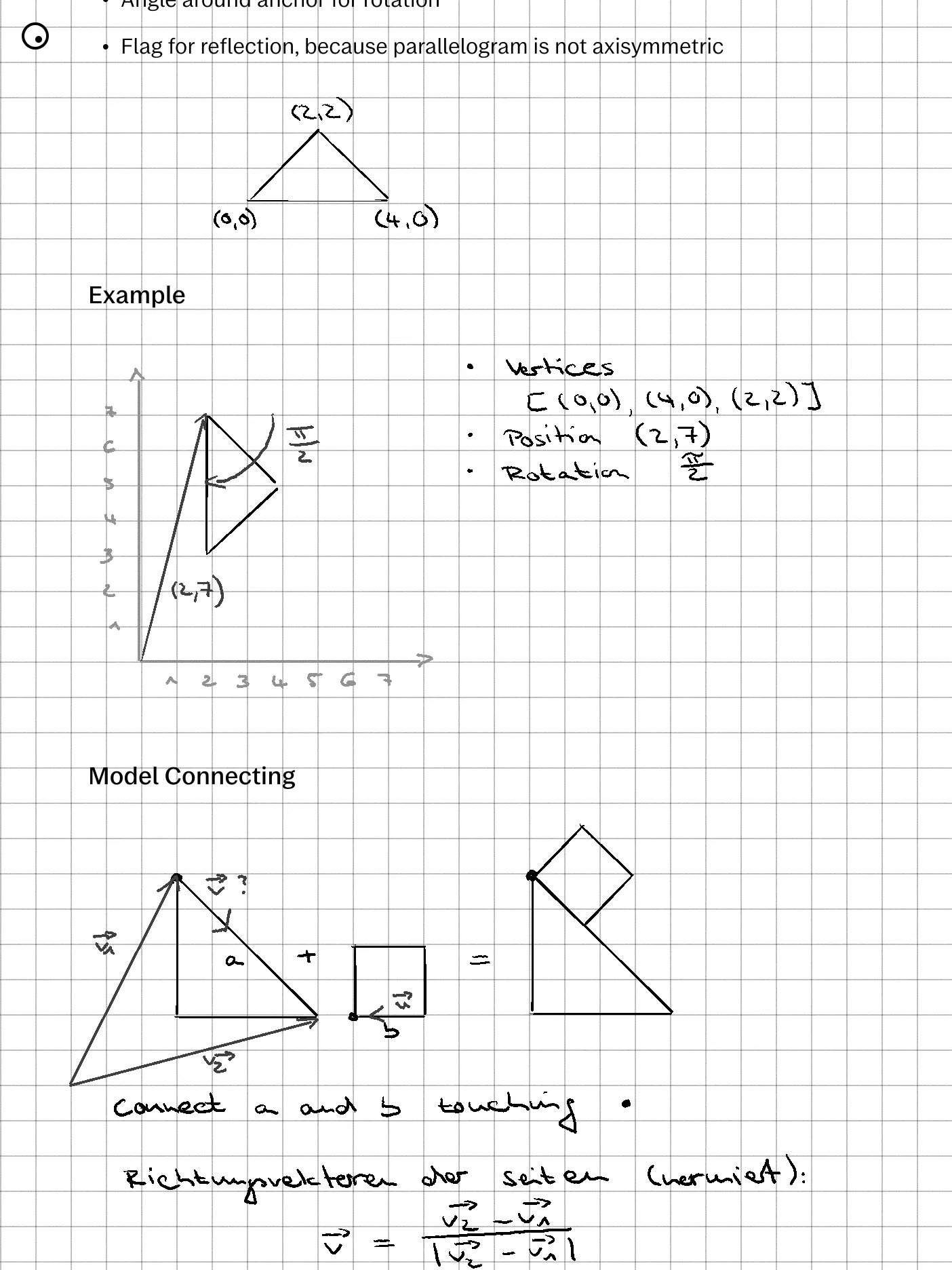
A screenshot from my first scribblings on my Remarkable.

Speaking of linear algebra: It was very valuable to think of vertices, sides, and directions as vectors. Everything in Tangram is a vector! The first vertex of every tan is the two-dimensional zero vector (0, 0) which serves as an anchor and rotation point for the whole shape. I set the square tan as the baseline for size with a side length of 1. That way the large triangle below would consist of the vertices [(0, 0), (2√2, 0), (√2, √2)]. I always start the list of vertices with the anchor and then proceed clockwise. Do not forget that when dealing with computer graphics, (0, 0) is in the top left corner of your canvas and the y-axis increases downwards.

The large triangle tan with a red dot that marks the anchor point (0, 0).
The red dot marks the anchor vector (0, 0).

And with that we can draw tans and configurations. The code below…

TTL1.position = createVector(1, -2);
TTL1.draw();

TTL2.position = createVector(1, -2);
TTL2.rotation = QUARTER_PI;
TTL2.draw();

TTM.position = createVector(1, -2);
TTM.rotation = HALF_PI;
TTM.draw();

TTS1.position = createVector(0, -1);
TTS1.rotation = -HALF_PI;
TTS1.draw();

TS.position = createVector(0, -1 - SQRT2);
TS.rotation = -QUARTER_PI;
TS.draw();

TP.position = createVector(0.5 * SQRT2, -1 - 1.5 * SQRT2);
TP.rotation = -HALF_PI;  
TP.draw();

TTS2.position = createVector(0.5 * SQRT2, -2.5 * SQRT2);
TTS2.rotation = -HALF_PI - QUARTER_PI;  
TTS2.draw();

…creates this swan configuration.

A stylized swan made of tans.

By the way, variable names like TTL1 will come up again. I am using the naming convention T for tan, then the first letter of the shape, then size, and a number. So TTL1 stands for tan triangle large one, or the first large triangle piece. TS would be the square, and so on.

2024-10-27: Connecting Tans

Laying out tans was fun, but messing with a lot of √2 and π not so much. I need better math and a better API to connect tans and create configurations.

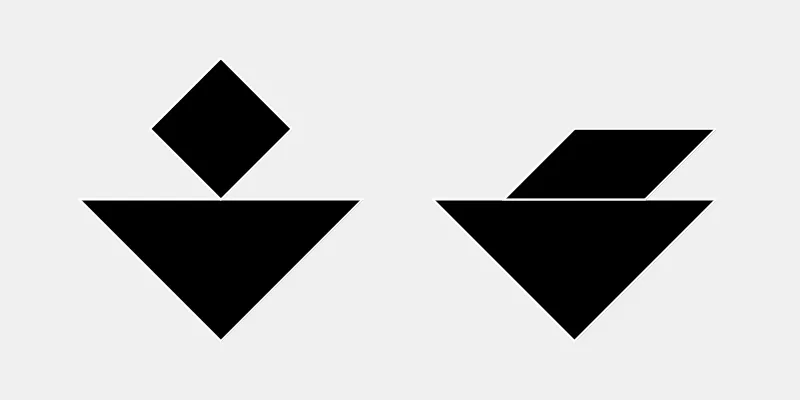
To make things a bit easier and manageable for now, I introduce two limitations for connecting tans:

  1. Tans only connect along sides. A touching vertex does not count as connecting.
  2. At least one vertex of each connecting side has to touch.

Given those two rules, the following examples are not valid connections. The left violates rule 1, the right rule 2.

Two examples for invalid connections.

Now I need to find out what steps in geometry are necessary to connect to tans and how to translate that into vector operations. Let’s look at an example.

A figure with six sub-images that are a visual recipe how to connect a large triangle piece with the square piece.

I want to connect side 1 of the square piece with side 2 of the large triangle piece. The figure above already contains some debug information that come in handy to grasp what’s going on. It is noteworthy, that sides are numbered clockwise (just like the vertices) and start with the corresponding vertex. So side 0 spans from vertex 0 to vertex 1. More generally, the directional vector that describes side x always points from vertex x to the next clockwise vertex x + 1 % |number of vertices|.

Connecting side 1 of the square tan (TS) with side 2 of the already placed large triangle tan (TTL) consists of four steps then (images 3–6 in the figure above):

  1. Move TS to the start vertex of side 2 of TTL.
  2. Rotate TS by the angle between TS’ side 1 and TTL’s side 2. Note that the two connecting sides point into opposing directions now.
  3. Move TS back by the distance between its anchor and the start vertex of its connecting side 1.
  4. Move TS along connecting side 2 of TTL by the length of its connecting side 1.

That’s it! Square and large triangle tans are now connected along side 1 and 2, respectively. I also introduced a flag endAligned that controls whether the connection aligns with the start (default, endAligned is falsy) or end (endAligned is truthy) vertex of the target side.

Two connections of the same tans, but one is end-aligned.
Left: start-aligned. Right: end-aligned.

That was a lot! It took me a bit to figure out the connection algorithm and turn it into vector operations, but it was worth it: The code to produce the same swan configuration from above is so much more readable and succinct now!

TTL1.translate(createVector(1, -2));
TTL1.connect(2, TTL2, 0, true);
TTL2.connect(2, TTM, 0);
TTM.connect(2, TTS1, 2);
TTS1.connect(1, TS, 0);
TS.connect(2, TP, 3);
TP.connect(0, TTS2, 2, true);

Gotta admit, it felt pretty amazing to watch those lines of code turn into a swan 😅.

2024-10-28: Cleanup, Collision, Configurations

My code needs some clean-up, so that’s what I am going to do. I also want to establish a class that models a configuration and build a static method on the Tan class that implements the Separated Axis Theorem allowing me to test whether two tans overlap each other. The video Convex Polygon Collisions by javidx9 was very helpful to wrap my head around this.

One can now build up a Tangram configuration by placing tans and I appreciate how the associated code mimics a game of Tangram in real life:

conf.place("TTL1");
conf.place("TTL2", 1, "TTL1", 0, true);
conf.place("TTM", 0, "TTL1", 1);
conf.place("TTS1", 1, "TTM", 1);
conf.place("TS", 2, "TTS1", 2);
conf.place("TP", 3, "TS", 0);
conf.place("TTS2", 2, "TP", 2);

All I have done today is mere prep work for the ultimate goal: Procedurally generating Tangram configurations! I feel I am getting somewhere here.

But the most important improvement is probably: color themes! I’ll leave you with yet another—but colorful—swan configuration.

Another stylized swan made of colored tans.

As always: Feel free to go nuts with my code in the p5.js web editor.

2024-10-31: Generating Random Configurations

All the bits and pieces are there, really. I just had to refactor some code, debug my isOverlapping method, and render many configurations by drawing onto p5.Graphics buffers rather than the main canvas.

Here are 100 randomly generated and valid Tangram configurations:

100 Tangram configurations layed out in a 10 by 10 grid.

There are some real beauties among them! Can you spot the climbing turtle? Or the blue whale? Or the Pyramids of Giza? Feel free to head over to my code for this update and play around with it.

It is surprisingly enjoyable to generate those configurations and let my mind read stories into the shadowy figures. But now I am wondering whether there is more.

Can I generate all configurations? (With my limitations in place, otherwise there would be infinite possibilities.) Bring back color in interesting ways? Experiment with other pieces? Genetic algorithms to produce more animal configurations? Or simply build a Tangram game? (With really juicy controls and effects!)

And so the creative part begins…

2024-11-02: Minor Observation

Interesting, how aesthetic merit depends on whether individual tans are visible or just the outlined shape. (Color also helps, to be fair.)

A star-like Tangram configuration that loses all its beauty when presented as an outline.

2024-11-04: Game Jam Submission and Future Work

I did it and submitted my procedural Tangram generator (procedural, not random, because I do set and check for some constraints) to PROCJAM 2024. That is more than I achieved last year and I am proud of my little piece of creative coding.

However, I would have liked to dig deeper into the topic of creating Tangrams with genetic algorithms. For that, I have worked through the Genetic Algorithms playlist on Youtube by Daniel Shiffman’s The Coding Train and the article Random Generation of Tangrams by Wiebke Köpp. The latter introduces some interesting ideas for future work and a couple of interestingness measures that could make for a good fitness function. But then the time ran out and I know I won’t have the bandwidth to work on this in the near future. All the better, that I managed to submit something to the game jam that allows me to consider this project done. My goal for next year: Submit more than just a proof of concept!

Some ideas for picking this up again in the future: